Ejercicios con pseudo código

¿Un algoritmo es similar a una expresión matemática?

Los algoritmos fueron, desde su origen hace tres mil años de antigüedad, operaciones matemáticas en secuencia para demostrar resultados. Es decir, evidenciar pasos comprobados y validados.

Practicando pseudocódigo

En esta sección propuse una sintaxis para diseño de pseudocódigo, con algunos términos en español, pero mantiendo ciertas palabras claves en sintaxis de lenguajes de programación, como Javascript.

Vamos con el primer y sencillo ejercicio:

Secuencia de números

Mostrar una secuencia de números, del 1 al 18, pero con incrementos de 3:

• 'Mostrar una secuencia' exige una iteración (repetición) de operaciones. La sintaxis FOR es adecuada en lenguajes de programación.
• Tener en cuenta que al actualizar el valor de 'num', se debe sumar lo que ese enlace ya tiene, más el valor de incremento (en este caso, el 3).
• La condición 'soloSi <= tope' solo recibirá a los números menores a 18, y ejecutará la actualización solo si esa condición se cumple en cada iteración.

INICIA Iteración del 1 al 18
num = 0, tope = 18;
FOR (con num, soloSi num <= tope, num = num + 3){
EsCierto:
 AhoraEs num = num + 3;
 Mostrar num;
}
//Interno num ahoraEs 0, 3, 6, 9....18
TERMINA

En sintaxis de Javascript, el ejemplo anterior se lo traduce en:

En Javascript

var num = 0;
var tope = 18;
for (num; num <= tope; num = num + 3){
    console.log(num);
}

Redondear cifra decimal

Aplicaremos solo matemática y el operador módulo (signo %) para extraer el residuo de una división.

• EL valor de 'cantDeci' nos permite indicar la cantidad de decimales finales

INICIA Redondeo de decimal
valor = 3.141699472;
cantDeci = 10;
preResultado = (valor * cantDeci) + 0.5;
ObtieneResiduoDiv = preResultado - (preResultado % 1);
resultadoFinal = ObtieneResiduoDiv / cantDeci;
Mostrar resultadoFinal;
FIN

Traducido a Javascript, el método toFixed(1) redondea la cifra a un decimal.

En Javascript

var valor = 3.141699472; 
console.log(valor.toFixed(1));
// 3.1

Identificar números primos

Recordémoslo: Un número primo solo tiene dos divisores con resultado entero positivo exacto (sin residuos): 1 y el mismo número. Donde divisible significa "puede dividirse exactamente, sin dejar fracciones".

Por ejemplo, el número 10 puede ser divisible para más números (para 10, para 5, para 2, para 1) y dar resultados sin residuos. Entonces el 10 no es primo, sino compuesto, porque tiene más de DOS divisores.

Pero lo especial viene aquí: el 11 es divisible para 11 sin dejar residuos; y el 11 es divisible para 1 sin dejar residuos. En toda la eternidad no existirán más números con los que podamos dividir 11 y dar un resultado únicamente entero (sin fracciones). Entonces, el número 11 es primo.

Indicado lo anterior, iniciaremos ensayando un pseudocódigo para identificar números primos según las características indicadas arriba:

INICIA identificar número primo
Pido n;
Si (n <= 1) entonces:
 Mostrar "Error. Ingresar mayor a 1";
 FIN
x = 2;
Mientras x <= raízCuadrada(n), hacer:
 Si (el residuo de n dividido para x es 0) entonces:
  Mostrar "No es primo";
  FIN (si la condición es cierta)
 Incrementar x en 1 (para seguir probando divisores);
 Sino (si no hay más divisores exactos), Mostrar "Es primo";
FIN

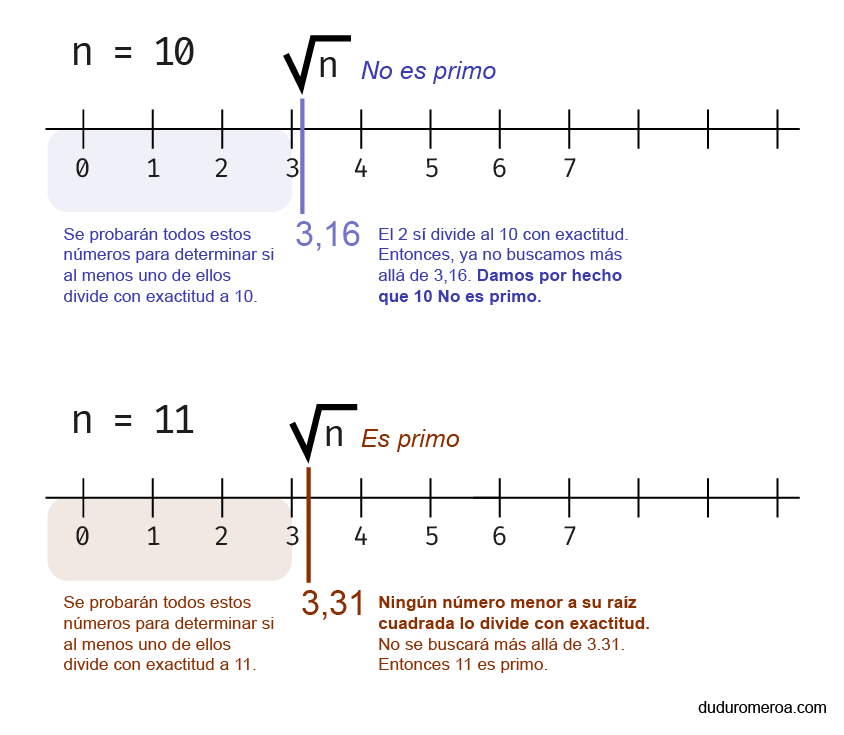
Nótese la necesidad de calcular un límite de operaciones, "hasta la raíz cuadrada de n", ¿por qué?. Recordemos que una raíz cuadrada es la operación inversa de una potencia. La raíz cuadrada de 25 es 5, pues 5 elevado a la 2 es 25. Luego, si n tiene un divisor menor que su raíz cuadrada, es muy posible que también tenga un divisor mayor a su raíz cuadrada. Y viceversa, si ningún número divisor pequeño funciona, no hace falta probar los números mayores a esa raíz de n.

Finalmente, la traducción en sintaxis Javascript del pseudocódigo anterior:

En Javascript

function esPrimo(n) {
    // Validación inicial
    if (n <= 1) {
        console.log("Error. Ingresar mayor a 1");
        return;
    }

    // Inicializamos el divisor
    let x = 2;

    // Bucle hasta la raíz cuadrada de n
    while (x <= Math.sqrt(n)) {
        if (n % x === 0) {
            console.log("No es primo");
            return; 
            // Termina la función si encontramos un divisor
        }
        x++; 
        // Fuera del bucle: 
        // Solo cuando todo lo anterior se haya evaluado...
        // Incremento X en 1
    }

    // Si ningún divisor fue encontrado para N, 
    // Entonces N es primo
    console.log("Es primo");
}

// Ejemplos
esPrimo(11); 
// Es primo
// 11 solo puede ser repartido (sin residuos)...
//... únicamente al dividirlo para sí mismo y para 1

Calcular espacios entre agujeros

Ejercicio tomado de Bird, J. (2010): Se perforan agujeros con una separación de 35,7 mm en una placa metálica. Si se perfora una fila de 26 agujeros, determine la distancia, en centímetros, entre los centros del primero y el último. Nota: Recordar que entre dos elementos existirá solo un espacio. Si por cada elemento le sigue un espacio, entonces por cada 5 elementos habría 4 espacios (haga la prueba el lector con cualesquiera elementos a la mano). Por lo tanto, en 26 elementos solo habrían 26-1 espacios.

Nota: Recordar que entre dos elementos existirá solo un espacio. Si por cada elemento le sigue un espacio, entonces por cada 5 elementos habría 4 espacios (haga la prueba el lector con cualesquiera elementos a la mano). Por lo tanto, en 26 elementos solo habrían 26-1 espacios.

INICIA CalcularEspacios
separacion = 35,7;
espacio = 26-1;
calculo = espacio * separacion;
 interno 892,5
convertirCm = calculo / 10;
 interno 89.25cm
Mostrar convertirCm;
FIN

En Javascript

// mm
separacion = 35,7;

// Por cada 2 elemenos habrá un solo espacio
// Si hay 26 elementos, solo habrán 25 espacios
espacio = 26-1;
calculo = espacio * separacion;
// 892,5

// Ahora preguntamos: 
// ¿Cuántos grupos de 10 existen en 892,5?
convertirCm = calculo / 10;
// 89.25

console.log("Hay una distancia 
entre el primero y último agujero de " + 
convertirCm + " cm");