¿Los algoritmos son únicamente para las computadoras?
La palabra algoritmo (derivada del árabe al Khowarizmi) refiere a un conjunto ordenado de acciones lógicas realizadas en un lapso limitado y alimentadas con información numérica para dar un resultado (nueva información). Hoy en día, el diseño de algoritmos es un amplio campo que propone mejores métodos para operar datos usando computadores.
No confundir algoritmo con logaritmo. Este último es una expresión matemática que representa a un valor multiplicado por sí mismo más de una vez (es decir, elevado a la potencia de un número mayor a 1) pero con una base numérica única. Por ejemplo, el logaritmo log2 8 = 3, se lee '8 en base (numérica) de 2 es igual a 3' (Soto Apolinar, 2011, p. 92)
Tampoco debemos confundir algoritmo con la palabra álgebra. Esta ha comprendido desde el siglo VIII a.C. hasta la actualidad un amplio estudio de las relaciones de igualdad matemática entre valores numéricos representados con literales. Por ejemplo, la igualdad 3a + 9a = 12a se cumplirá siempre que el valor de 'a' sea reemplazado con cualquier número entero mayor a 1.
¿Cómo resultaría aplicar un algoritmo en la cotidianidad de una persona? un estudiante que desee mejores calificaciones (un objetivo muy general) logrará poco si carece de acciones o pasos precisos. Un objetivo menos ambiguo sería alcanzar puntajes de entre 9 a 9.5 puntos, por ejemplo.
Sin embargo, los seres humanos debemos contar con mucha fuerza de voluntad y disciplina para ser ordenados y lógicos. A diferencia de un equipo electrónico que sigue secuencias, los seres humanos contamos con otras fuerzas de motivación emocional y mental para lograr (o desistir, o demorar) nuestras metas personales.
Los algoritmos también permiten diseñar acciones alternas en caso de que una tarea planeada no sea ejecutada. Por ejemplo, cuando el usuario de un cajero automático espera demasiado tiempo para recibir su dinero. En ese caso, el algoritmo interno debería alertar y comunicar al usuario la razón de esa demora. El diseñador del algoritmo debería entonces prever los siguientes infortunios en el funcionamiento del cajero:
- Una conexión pausada
- El usuario ya no tiene dinero en el banco
- La cifra de retiro es incorrecta
- Demora en los cálculos del sistema
- Causa desconocida
Condiciones a cumplir de un algoritmo
Según lo explicado por Horowitz, Sahni y Rajasekaran (1999, p. 1), un algoritmo ejecutado por un sistema electrónico cumple con lo siguiente:
- Tiene inicio
- Recibe y crea nuevos datos en forma de números. Esos resultados están relacionados con los datos ya ingresados.
- Sus acciones son precisas (un evento realiza una única acción, sin interpretaciones ni confusiones de significado).
- Sus acciones son ejecutables en cualquier contexto de uso (por ejemplo, el mismo algoritmo debe poder usarse en todas las operaciones aritméticas).
- Tiene Fin
Otros autores (Duque, Velásquez, Segovia y Loaiza, 2017, p. 37) mencionan tres acciones mínimas y necesarias que debe contener un algoritmo:
- Inicio
- Capturar, conocer o ingresar todos los datos que permitan resolver el problema.
- Resolver, calcular o llevar a cabo los procesos con los datos capturados. Se sugiere en este punto colocar las ecuaciones necesarias.
- Mostrar, visualizar o imprimir todos los resultados que el problema exi- ja.
- Fin
Un algoritmo puede agrupar breves tareas o una lista extensísima de ellas, pero todas tendrán un límite, un inicio y un fin. Y serán lógicas, es decir, tendrán estrecha relación con el resultado y su consecuencia. Así mismo, un algoritmo debe ser susceptible de ser ejecutado una sola vez o miles de veces.
Para prever todo eso tenemos a disposición el diseño de algoritmos, ya sea con diagramas o pseudocódigo para así entender cómo "llega [una máquina] a su resultado" (Barnett, Del Tongo, 2008, p. 7) antes de aplicar sintaxis de programación y llevarlo al mundo real.
Diagramas, pseudocódigo y simbología
Un pseudocódigo es una forma de representación visual sin ejecución electrónica. Es una lista de tareas lógicas y en secuencia, elaboradas a lápiz y papel o mediante básicas expresiones verbales que representan operaciones para hallar o alterar datos, pero sin ser aún ejecutadas por un computador. Esa lista permitirá evaluar y corregir la eficacia o potenciales fallos en el diseño de tareas lógicas, como lo es un algoritmo.
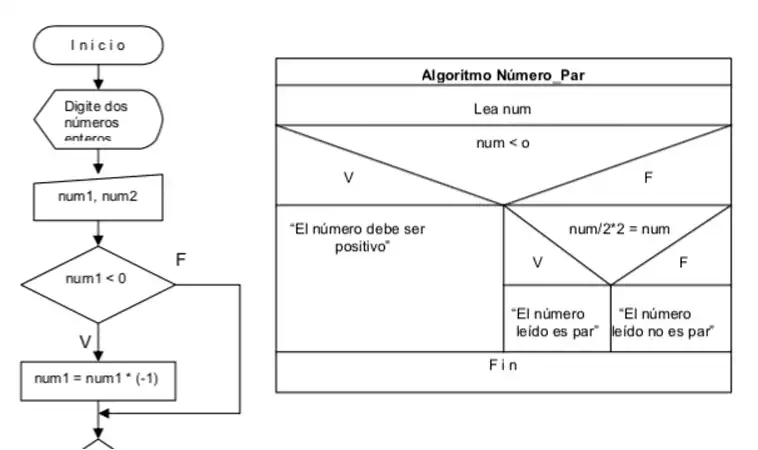
Otras formas de representar algoritmos son mediante diagrama de flujo, o con diagramación rectangular estructurada (Trejos, 1999, p. 99-100 ), o con pseudocódigo, el único método que se profundizará más adelante.
Objetivo de un pseudocódigo
Su objetivo es definir qué debe resolverse claramente y cuál es el orden de una o más acciones para obtener un resultado (como un proceso aritmético en finanzas o en ciencias de probabilidad). El algoritmo deberá ser fácil de evaluar mucho antes de plantearlo y ejecutarlo desde una sintaxis de lenguaje de programación, y desde una máquina.
La historia técnica del diseño de pseudocódigos (que inició a la par de los primeros computadores electrónicos en la década de 1950, en Europa y EE.UU.) ha establecido varias simbologías para su diseño.
Sintaxis o simbología técnica para crear pseudocódigos
Una breve revisión bibliográfica (ver lista de libros consultados, al final de este texto) me permite llegar a esta conclusión: no existe una única sintaxis para diseñar pseudocódigos. En algunos casos, cada sintaxis ha estado basada en la de cierto lenguaje de programación, como C++ o C#; y con añadidos como el mostrar las precondiciones que los datos deben contener (Barnett, Del Tongo, 2008, p. 4). Otros autores muestran una sintaxis de pseudo código diferente.
A pesar de esas diferencias, esas variantes tienen algo en común: todas muestran una secuencia de tareas bien definidas que facilitan comprender "cómo piensa" el algoritmo y certifican el resultado buscado.
Sintaxis genérica para diseñar y estucturar pseudocódigo
En la tabla de abajo, los dos primeros literales (A, B) se comportan como contenedores o enlazadores de datos (también llamados variables y constantes). En programación, son identificadores en forma de letras o palabras que enlazan a datos, como letras, números enteros o decimales, valores lógicos de Verdad (True) o Falso (False), o valores nulos.
La tabla siguiente está basada en simbología para pseudocódigo, revisada en Barnett, Del Tongo (2008, p. 101); Duque, Velásquez, Segovia, Loaiza (2017, p. 41 en adelante). Nota: Me inspiré en esta tabla para proponer (al final de este artículo) una alternativa de sintaxis para pseudocódigo.
Significa |
|||
| A ➔ B + (X*Y) |
Flecha de asignación: Primero resolver B + (X*Y) y luego enlazar ese resultado en A |
||
| A ➔ A + Y |
Flecha de asignación: Resolver A + Y y alojarlo en A |
||
| A ➔ B |
Flecha de asignación: Alojar el valor de B en una variable A |
||
| A == B |
Compara: el valor alojado en A es idéntico al valor alojado en B |
||
A = B |
A es igual a B |
||
n |
Cualquier número |
||
A*B |
Multiplicar A por B |
||
A/B |
Dividir A para B |
||
A && B |
Similar al operador lógico Y (A y B) |
||
A || B |
Similar al operador lógico Ó (A ó B) |
||
A++ |
Incrementar el valor de A en 1 |
||
for (A=0; B>A; A++){ A+1} |
Repetir la suma A+1 siendo que A inicie con el valor de cero, evaluar que B sea mayor que A; luego, sumar A+1 y finalmente incrementar A en 1 unidad. |
||
Read (A, B) |
El usuario debe agregar datos para cada literal o enlace. Se entiende que el sistema almacena esos valores para luego operarlos. |
||
Write (A, B) |
Mostrar, visualizar o imprimir en un soporte los resultados o valores de A. |
||
If (A > B) then |
Condicional Sí...entonces |
||
Do (A++) While A > B |
Iteración: Hacer mientras condición A > B sea verdad |
||
else (A == B) |
Estado falso de condición if, ó 'de lo contrario' |
||
return (A) |
Entrega el resultado de A, pero hacia dentro del sistema para que otras operaciones puedan usarlo. Es decir, retorna valores entre funciones y operaciones. No es una salida en pantalla, como Write. |
||
if ... end if |
Indica inicio y fin de condicional if |
||
if ... end if |
Indica inicio y fin de condicional if |
Igualdad, comparación y asignación. Diferencias
En pseudocódigo y en lenguajes de programación, el signo '=' representa una igualdad; es decir, un valor contenido en una entidad (llamada también variable).
Así mismo, el signo '==' representa una igualdad por comparación. Es decir, donde valores o expresiones tendrán valores idénticos uno con el otro.
En algunas convenciones de pseudocódigo, la asignación está indicada con la flecha invertida a la izquierda, por ejemplo, donde el valor de 100 será asignado a la variable 'number': number ➔ 100. Considero que esa símbolo debería ser reemplazado por algún otro que indique similar asignación (o enlace) de un valor.
El pseudocódigo de abajo (con sintaxis para pseudocódigo usada en bibliografía revisada) indica lo siguiente: cualquier 'n' número alojado en 'num' será dividido para dos y multiplicado por dos. La igualdad entre los valores de los enlaces 'num' y 'opera' siempre se producirá.
- Inicia
- Lee num ➔ n
- Escribe n
- opera ➔ (n / 2) x 2
- If (num == opera) then...
- Mostrar 'Ambos son iguales'
- Si no, mostrar 'Error. No son iguales'
- Fin
La traducción a lenguaje de Javascript es la siguiente:
En Javascript
var num = -0.000000123;
var opera = num / 2 * 2;
if (num == opera){
console.log("Ambos son iguales");
} else
{console.log("Error. No son iguales");
}
// Ambos son iguales
El que un algoritmo tenga un final definido es importante en programación, puesto que conlleva a que deberá ser ejecutado durante un lapso máximo. Por ejemplo, el lenguaje Javascript exige el punto y coma para indicar que una expresión tiene un inicio y un final. Y en los tipos de datos llamados funciones, la sentencia return indica que la función debe finalizar luego de ejecutar las instrucciones que contenga esa función.
En Javascript
function saludar(x){
// Aquí termina función
return x;
// pero...
console.log("Esto NO SERÁ ejecutado!");
}
console.log(saludar("Hola Dudu"));
// Hola Dudu
// ...
// Esta expresión finaliza con el punto y coma.
// Es decir, solo se hará la resta y nada más!
let calcularEdad = 2024-1976;
console.log(calcularEdad);
// 48
Planear y diseñar un algoritmo (mediante pseudocódigo, diagrama de flujo u otros) son acciones independientes del lenguaje de programación que podría ser usado luego usado para ejecutar ese algoritmo. Es decir, si funciona en pseudo código, antes de aplicarle la sintaxis de un lenguaje de programación, entonces funcionará en máquina.
Mi crítica acerca de cómo se ha representado tradicionalmente la sintaxis de un pseudocódigo
Entender un solo lenguaje de programación no es una tarea fácil. Su sintaxis y micro sintaxis es un muy extenso diccionario de combinaciones de palabras, recortadas o incompletas, justamente para no ocupar demasiadas líneas de código al elaborar una secuencia de tareas. Además de eso, cada cierto tiempo uno o más lenguaje ajustan, reducen o extienden su diccionario de sintaxis. A pesar de eso, todo lenguaje de programación permitirá y producirá las siguientes acciones:
- Dar por hecho que un dato existe y se puede usar
- Dar por hecho que un dato puede o no ser alterado o actualizado
- Alojar datos en memoria electrónica
- Enlazar datos con nombres identificadores fáciles ubicar
- Operar matemáticamente
- Mostrar los datos o sus combinaciones
- Agrupar instrucciones repetibles con diversos datos
- Permitir desvíos mediante comprobación de condiciones lógicas (como Sí, No, Falso, Verdad) y dar resultados según cada condición.
Es decir, todas las anteriores acciones también pueden ser reseñadas mediante frases y operaciones de una lista de tareas desde un pseudocódigo, incluso si decidimos no usar aún un lenguaje de programación.
Por lo tanto, ¿por qué no se ahonda primero en la práctica de algoritmos con pseudocódigos? Quizás por que sentimos que aprender un lenguaje de programación es la vía directa, o por que pensar en algoritmos requiere banal esfuerzo de abstracción, o porque carece de los fuegos pirotécnicos audiovisuales en pantalla. Sin embargo, practicar pseudocódigo es necesario para pensar con lógica y en secuencia, no exige encender el computador. Solo lápiz y papel; o pizarra y tiza; y por su puesto nuestra atención mental.
En otros casos, la sintaxis propuesta para ejercitar pseudocódigo podría ser desconocida o poco intuitiva. En mucho ejemplos hallados (en la bibliografía, abajo) la forma de expresar pseudocódigo está basada en una tradición académica estadounidense iniciada desde mitad del siglo XX, cuando las gigantes computadoras UNIVAC empezaron a interpretar los primeros lenguajes de máquina, como Flow-Matic, desarrollado por la docente estadounidense Grace Hooper (1906-1992), entre 1955 y 1959; y Cobol (1965). Estos lenguajes requerían usar (y abreviar) palabras en inglés para evitarles a otros nuevos usuarios el uso de excesiva notación científica, confusa para no expertos en matemáticas.
Es así que los primeros pseudocódigos nacieron de explicar el uso de esos lenguajes a nuevos usuarios (especialmente a empresas o instituciones universitarias) utilizando palabras simples como (aquí en español): COMPARAR, TRANSFERIR, ESCRIBIR, MOVER, LEER, SALTAR A, EVALUAR, RETROCEDER, DETENER, FINAL, entre otros.
Por todo lo anterior ensayo aquí una sintaxis para pseudocódigo. Usaré convenciones en inglés (para mantener el tono común en lenguajes de programación) pero rescataré términos en español para ciertas acciones.
Omitiré flechitas como A ➔ B (enlazar el valor de B en A); muy común en notación académica técnica, pero ligeramente poco práctico para nuestra lectura de izquierda a derecha. Lo reemplazaré con el signo = para indicar asignación, y doble == para indicar igualdad simple.
Propuesta de nueva sintaxis para pseudocódigo
Basándome en lo revisado en Barnett, Del Tongo (2008, p. 101); Duque, Velásquez, Segovia, Loaiza (2017) y demás bibliografía pertinente, muestro acá una propuesta de sintaxis de pseudocódigo para ejercicio de algoritmos (no complejos) de iteración, bucles, enlace de datos y operaciones aritméticas. Mostraré actualizaciones en caso de ser necesario o al evaluarlo con ejercicios.
He eliminado las flechas (a la izquierda o a la derecha, me da igual, simplemente ya no son pertinentes). Ni hablar del raro signo ::=<.
Así mismo, mantengo el signo = solo para asignaciones (ojo, no para igualdad); los signos == para evaluar igualdades; y el punto y coma para cerrar o finalizar cada expresión. Todos ellos símbolos ya estándar en programación.
| Expresión | Cómo aplicarla | ||
| INICIA, TERMINA | Tal cual son usados para indicar qué inicia y qué finaliza. | ||
| Existe A, B; | Para declarar enlaces en caso de no desear inicializarlos (es decir, crearlos sin valores). Representa el uso de los operadores VAR, LET, CONST, de Javascript. | ||
| = | Para vincular una asignación de valores con su enlace. El uso del signo 'igual a' en progamación permite inicializar (dar un valor de inicio) a un enlace, como en la forma VAR NUM = 20; en Javascript. Cuidado: en este contexto el signo 'igual' no representa una igualdad. | ||
| == | Doble signo 'igual' para evaluar similitud de valores. Como en la forma NUM == 20; (donde solo será Verdad si ambos son iguales). |
||
| A || B | Operador lógico común en lenguajes de programación. Representa el booleano ó: como en (A Ó B). | ||
| A && B | Operador lógico, representa el booleano Y: como en (A y B). | ||
| A ahoraEs B | Representa únicamente una actualización o reasignación del valor del enlace. Para asignación común, usar el signo igual (=). | ||
| if (A==B){
esCierto: (aquí operación) } else { esFalso: (aquí operación) } |
Condicional común en lenguajes de programación, donde la afirmación entre paréntesis deberá ser de certeza (TRUE) para ejecutar el código dentro de la condicional. Si es falso, sigue a else. | ||
| Pido X; | En caso que se permita al usuario ingresar un dato, previo a su declaración en la forma Existe X; | ||
| Mostrar A; Mostrar "Son iguales"; | Para mostrar o hacer visible un dato o texto hacia el usuario. | ||
| //Interno Ahora es B + 10 | Operación interna de los cálculos del pseudocódigo. En lenguajes de programacón no es una operacion visible. Las barras // representan el modo de comentario en el lenguaje Javascript. | ||
| Listo A; | Representa al operador return. Alista un resultado (generalmente de una función) para ser usado luego. | ||
| Detener bucleA | En caso de bucle, 'Detener es la pausa de este. Representa al break de un bucle. | ||
| Con i desde 0 hasta 5 ... FinCon | Con y Fin representa a la sintaxis de un bucle FOR. | ||
| A > B, A >= B, A + B, A * B, A / B. Y para agrupar operaciones (A + B), etcétera. | Símbología común para álgebra y matemáticas. |
Finalmente, usaré la sencilla propiedad transitiva de igualdad aritmética como ejercicio. Prometo "meter al fuego" la sintaxis propuesta, y evaluarla, afinarla o mejorarla.
Existe A;
Existe B;
Existe C;
A AhoraEs 10;
B AhoraEs 10;
C AhoraEs 10;
if A == B && B == C && C == A
Mostrar esto: "Son iguales";
if Termina
Deseo que estudiantes más jóvenes, incluso colegiales mejoren (mucho mejor si lo mejoran) mi propuesta de pseudocódigo, y así reducir la distancia que aún existe en nuestros estudiantes (de cualquier condición económica o social) con el aprendizaje de los fundamentos en tecnología y programación.
Puedes escribirme a mi mail si consideras que ese aporte necesita un ajuste o mejoramiento. Estaré gustoso de publicar tu observación.
Ensayaré la sintaxis de pseudocódigo aportada con más ejemplos en la siguiente sección.
BIBLIOGRAFÍA
Barnett, G., Del Tongo, L. (2008) Data Structures and Algorithms: Annotated Reference with ExamplesCormen, T., Leiserson, Ch., Rivest, R., Stein, C. (2022) Introduction to Algorithms (4ta. Ed.) MIT press.
Duque, D., Velásquez Saint-Priest, Segovia P., Loaiza F. (2017) Algoritmos y programación en pseudocódigo. Editorial Universidad Santiago de Cali.
Horowitz, E., Sahni, S., Rajasekaran, S. (1999) Computer algorithms Computer Science Press, W. H. Freeman.
Knuth, Donald, E. (1997) The art of computer programming. 3ed. Vol. 1. Addison Wesley Longman ed.
Neapolitan, R. (2015) Foundations of Algorithms Jones, Bartlett Learning Press.
Soto Apolinar, Efraín (2011) Diccionario ilustrado de conceptos matemáticos. 3ed edición. México.
Trejos, B. Omar (1999) La esencia de la lógica de programación. Editorial Papiro. Colombia.